Переключите год учебника.
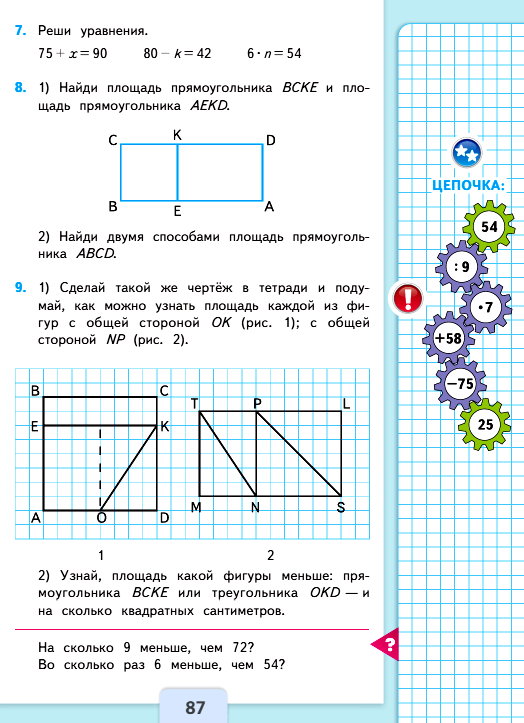
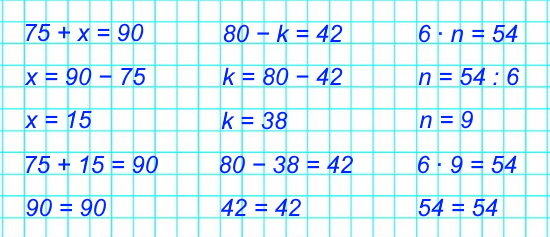
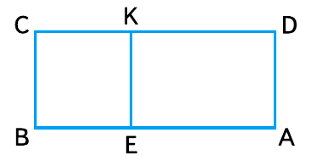
1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди площадь прямоугольника ABCD. Сколькими способами это можно сделать?

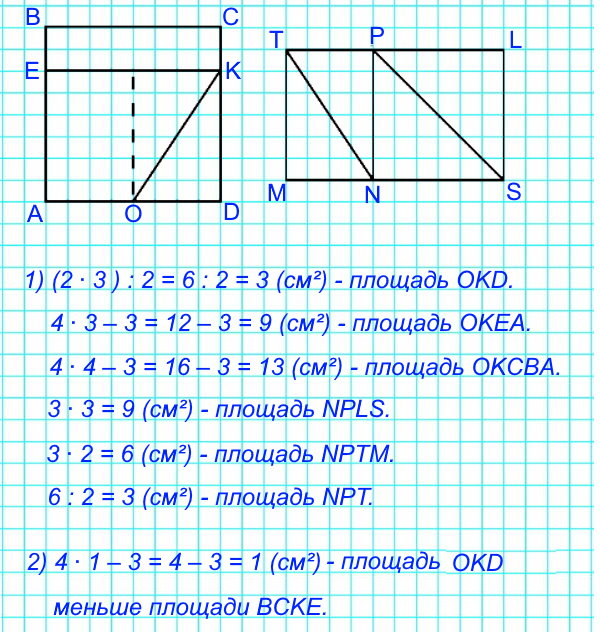
1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP (рис. 2).
Пояснение:
1) Общая сторона OK есть у трёх фигур:
- треугольника OKD
- четырехугольника OKEA
- пятиугольника OKCBA
(2 ∙ 3 ) : 2 = 6 : 2 = 3 (см²) – площадь треугольника OKD.
4 ∙ 3 – 3 = 12 – 3 = 9 (см²) – площадь четырехугольника OKEA.
4 ∙ 4 – 3 = 16 – 3 = 13 (см²) – площадь пятиугольника OKCBA.
Общая сторона NP есть у четырёх фигур:
- квадрата NPLS
- прямоугольника NPTM
- треугольника NPT
- треугольника NPS
3 ∙ 3 = 9 (см²) – площадь квадрата NPLS.
3 ∙ 2 = 6 (см²) – площадь прямоугольника NPTM.
6 : 2 = 3 (см²) – площадь треугольника NPT.
9 : 2 (см²) – площадь треугольника NPS.
2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD – и на сколько квадратных сантиметров.
4 ∙ 1 – 3 = 4 – 3 = 1 (см²) – площадь OKD меньше площади BCKE.
На сколько 9 меньше, чем 72? Во сколько раз 6 меньше, чем 54?
72 – 9 = 63
54 : 6 = 9 (раз)
ЦЕПОЧКА:
54 : 9 = 6
6 · 7 = 42
42 + 58 = 100
100 – 75 = 25

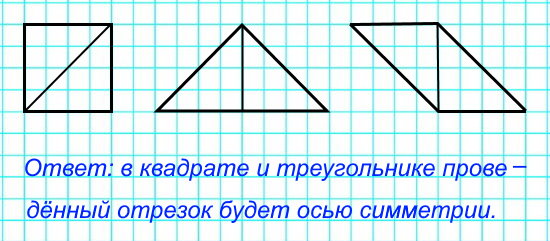
В каких фигурах проведённый отрезок будет осью симметрии фигуры?

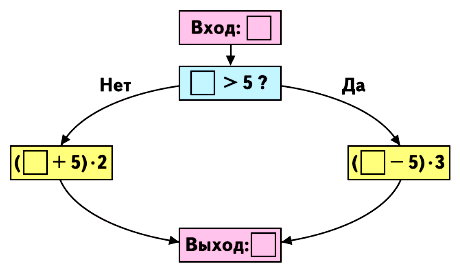
1) Какое число будет получаться на выходе из машины, если в неё ввести число: 3, 8, 2, 11, 14?
2) Какое число ввели в машину, если на выходе из машины получили число 3?
- (3 + 5) · 2 = 16
(8 – 5) · 3 = 9
(2 + 5) · 2 = 14
(11 – 5) · 3 = 18
(14 – 5 ) · 3 = 27 - 3 : 3 = 1 + 5 = 6
6 > 5 – да
(6 – 5) · 3 = 3