ГДЗ - МАТЕША.РФ

Учебник Моро 3 класс. 1 часть. Страница 74

Страница 74

Отличаются задания?
Переключите год учебника.


№1. Начерти такие фигуры в тетради.

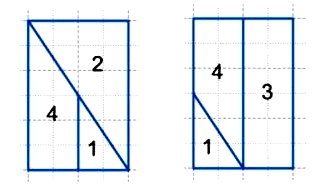
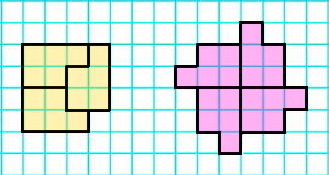
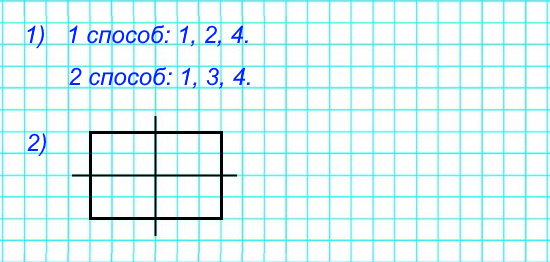
1) Раздели фигуру 1 на три равные части так, чтобы линии деления шли по сторонам клеток.
2) Раздели фигуру 2 на четыре такие же части, как в предыдущем задании. Линии деления также должны идти по сторонам клеток.

№2. Три друга: Кирилл, Алексей и Глеб – участвовали в теннисном турнире. Один из этих мальчиков стал победителем турнира. На вопрос: «Кто победил?» – Кирилл ответил: «Это не я». Алексей сказал: «Победителем стал Глеб». Позже выяснилось, что один из этих ответов верный, а другой нет. Кто победил в теннисном турнире? Начни рассуждать так: «Предположим, что Алексей сказал правду, тогда и Кирилл…»

Предположим, что Алексей сказал правду, тогда и Кирилл сказал правду — это невозможно, так как одно из утверждений верно, а другое — нет.

Значит правду сказал Кирилл, а не Алексей. Значит, победителями не могли быть ни Глеб, ни Кирилл.

Ответ: победил Алексей.

№3. Мальчик купил несколько булочек по 17 р. Он подал в кассу 100 р. и получил сдачу в виде нескольких пятирублёвых монет. Сколько пятирублёвых монет он мог получить?

Так как мальчик получил сдачу в виде пяти рублевых монет, значит общая сумма сдачи должна делиться на 5 без остатка, а значит и сумма покупки должна делиться на 5 без остатка.

Тогда:

1) 17 ∙ 5 = 85 (руб.) − составила общая сумма покупки;
2) 100 − 85 = 15 (руб.) − составила сдача;
3) 15 : 5 = 3 (монеты) − получил мальчик.

Ответ: 3 пятирублевые монеты.

№4. Используя в каждом случае 4 раза цифру 7, знаки арифметических действий и, если надо, скобки, составь 5 выражений со значениями: 5, 6, 7, 8, 9.
Например: 7 – (7 + 7) : 7 = 5.

7 – (7 + 7) : 7 = 5
(7 · 7 – 7) : 7 = 6
(7 – 7) · 7 + 7 = 7
(7 · 7 + 7) : 7 = 8
(7 + 7) : 7 + 7 = 9

№1. В новом пятиэтажном доме 80 квартир. На каждом этаже заселили по 8 квартир. Сколько квартир осталось заселить?

Всего – 80 кв.
Заселили – 5 эт. по 8 кв.
Осталось – ? кв.
1) 8 · 5 = 40 (кв.) – заселили.
2) 80 – 40 = 40 (кв.)
Ответ: 40 квартир осталось заселить.

№2. Поставь вопрос так, чтобы задача решалась двумя действиями; реши задачу.

1) В школьном дворе росло 12 берёз, а рябин в 4 раза меньше. Сколько деревьев росло в школьном дворе?

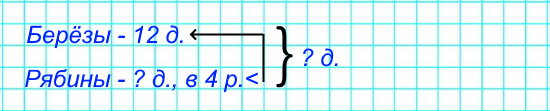
1) 12 : 4 = 3 (д.) – рябины.
2) 12 + 3 = 15 (д.)
Ответ: 15 деревьев росло в школьном дворе.

2) На первом этаже школы 9 учебных помещений, а на втором – на 2 больше. Сколько помещений на двух этажах школы?

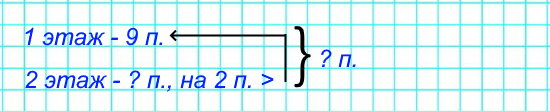
1) 9 + 2 = 11 (п.) – на втором этаже.
2) 9 + 11 = 20 (п.)
Ответ: 20 помещений на двух этажах.

3) На строительстве дома работали 10 плотников, а маляров в 2 раза больше. Сколько человек работало на стройке?

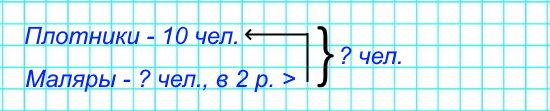
1) 10 · 2 = 20 (чел.) – маляры.
2) 10 + 20 = 30 (чел.)
Ответ: 30 человек работало на стройке.

№3. В магазин привезли фрукты в ящиках: яблоки – по 9 кг в ящике, а груши – по 8 кг в ящике. Объясни, что означают выражения.

9 + 8 = 17 (кг) − столько груш и яблок в двух ящиках.
9 ∙ 3 = 27 (кг) − масса 3 ящиков яблок.
8 ∙ 4 = 32 (кг) − масса 4 ящиков груш.
8 ∙ 4 + 9 = 41 (кг) − масса 4 ящиков груш и 1 ящика яблок.
9 ∙ 3 + 8 = 35 (кг) − масса 3 ящиков яблок и 1 ящика груш.

№4. Какие из чисел от 42 до 63 делятся на 7 без остатка?

42 : 7 = 6
49 : 7 = 7
56 : 7 = 8
63 : 7 = 9

Ответ: 42, 49, 56, 63.

№5. Может ли частное быть равно делимому? Приведи пример.

Да, может, если делитель равен 1 или делимое равно 0.

9 : 1 = 9
0 : 8 = 0

№6.

№7. 8 карандашей стоят 72 р. 1) Сколько стоят 7 таких карандашей? 2) Сколько таких карандашей можно купить на 20 р.? Сколько денег останется?

1) 72 : 8 = 9 (р.) – стоит 1 карандаш.
2) 7 · 7 = 49 (р.) – стоят 7 карандашей.
3) 9 · 2 = 18 (р.) – стоят 2 карандаша.
4) 20 – 18 = 2 (р.)
Ответ: 49 рублей стоят 7 карандашей; 2 карандаша можно купить на 20 рублей, 2 рубля останется.

№8. Периметр треугольника 48 см. Длина одной его стороны 16 см, а другой – 18 см. Найди длину третьей стороны этого треугольника.

Периметр – 48 см
Длина сторон – 16 см и 18 см
Осталось – ? см

1) 16 + 18 = 34 (см) – длина двух сторон треугольника.
2) 48 – 34 = 14 (см)
Ответ: 14 сантиметров длина третьей стороны треугольника.

№9. 1) Из каких трёх фигур можно сложить прямоугольник? Запиши их номера. Сколькими способами можно это сделать?
2) Начерти такой прямоугольник и проведи в нём оси симметрии.

1) Из каких трёх фигур можно сложить прямоугольник? Запиши их номера. Сколькими способами можно это сделать? 2) Начерти такой прямоугольник и проведи в нём оси симметрии.

ПОЯСНЕНИЕ:

<< Стр 73Стр 74Стр 75 >>

Выбрать другую страницу

Поделитесь ответами с друзьями
Подпишитесь на нашу группу вк!